在现代信号处理领域，如何有效地从噪声中提取有用信息一直是研究的热点。特别是在处理非线性、高维信号时，传统的线性方法往往力不从心。基于此背景，梯度流的扩散映射卡尔曼滤波算法（GFDMKF）应运而生，成为一种前沿的信号预处理技术。本文将通过MATLAB仿真，深入探讨这一算法的实现及其在不同噪声环境下的表现。

算法简介

GFDMKF结合了扩散映射（Diffusion Maps）和卡尔曼滤波的优势，通过非线性流形学习捕捉数据的内在结构，并利用梯度流优化滤波过程。扩散映射通过构建数据点之间的相似性矩阵，将高维数据映射到低维空间，保留了数据的本质特征。随后，卡尔曼滤波在这一低维空间中进行状态估计，利用梯度流进一步优化预测和更新步骤，提高了对非线性动态系统的适应性和估计精度。

MATLAB仿真设置

在MATLAB环境中，我们首先加载数据并设置参数：

load data.mat
SNR = 10;  % 信噪比
Dims = 2;  % 扩散映射坐标使用的维度
Ts = 0.01; % 时间步长

接着，我们生成含噪声的测量值，并通过扩散映射和卡尔曼滤波进行处理：

x0 = atan(ang1./ang2).';  % 清洁角度值
y0 = sqrt(ang1.^2 + ang2.^2).'; % 清洁半径值
x1 = awgn(x0, SNR, 'measured'); % 含噪声角度
y1 = awgn(y0, SNR, 'measured');  % 含噪声半径

结果展示与分析

通过仿真，我们可以观察到不同信噪比（SNR）下的滤波效果。以下是部分代码展示如何绘制结果：

figure
scatter(tt * Ts, y1, 20, [0.75, 0.75, 0.75], '.'); % 绘制噪声半径测量点
hold on
plot(tt * Ts, y0, 'g:', 'LineWidth', 2); % 绘制清洁半径轨迹
plot(tt * Ts, y_est(2, tt), 'r', 'LineWidth', 1); % 绘制DMK估计的半径轨迹
xlabel('t/s');
ylabel('r')
legend('含噪声测量信号', '无噪声测量信号', '扩散映射卡尔曼滤波');

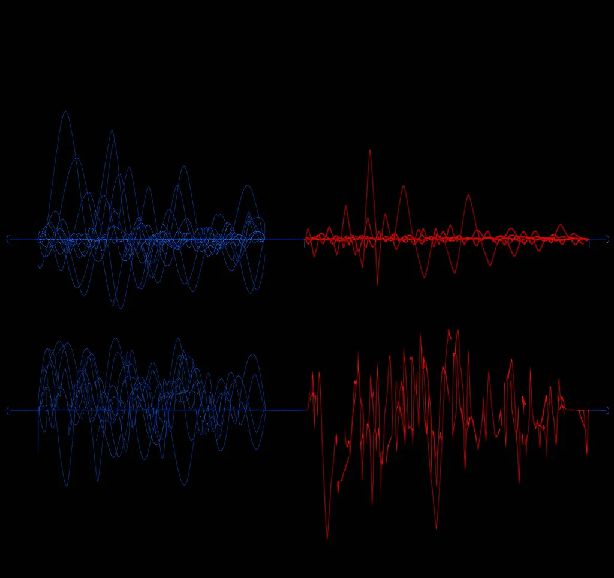
从图中可以看出，GFDMKF算法在处理含噪声信号时，能够有效地恢复出接近原始信号的轨迹，显示出其在非线性信号处理中的强大能力。

算法原理深究

1. 扩散映射：通过构建数据点间的扩散核（如高斯核），将高维数据映射到低维空间，保留数据的几何结构。

2. 卡尔曼滤波：在低维空间中，利用卡尔曼滤波进行状态估计，预测和更新步骤通过梯度流优化，适应非线性变化。

3. 梯度流优化：通过梯度下降法调整参数，使得滤波过程更加贴合数据的真实分布，提高估计的准确性。

应用前景

GFDMKF不仅在理论研究中具有重要意义，在实际应用中也展现出广阔的前景。例如，在金融市场预测、气象数据分析、生物医学信号处理等领域，都可以利用这一算法进行高效的信号预处理和状态估计。

结论

通过MATLAB仿真，我们验证了基于梯度流的扩散映射卡尔曼滤波算法在信号预处理中的有效性和优越性。该算法不仅能够处理高维、非线性信号，还能在噪声环境下保持较高的估计精度，为信号处理领域提供了一种新的思路和方法。

通过本文的探讨，读者可以进一步了解如何在MATLAB中实现和应用GFDMKF算法，并在自己的研究或实际应用中加以利用，推动信号处理技术的不断进步。